
Wet van Benford: feit of toeval?
De ontwikkeling loopt nog, maar we willen alvast wat meer vertellen over de functionaliteiten van het aankomende Caseware Analytics AI. Analytics AI maakt gebruik van verschillende algoritmes om risico’s en transacties te analyseren en fraude op te sporen. Met deze blog willen we inzoomen op een van de tests die hierin gebruikt wordt: de wet van Benford.
Velen van jullie zullen wel eens gehoord hebben van de wet van Benford of deze wel eens toepassen in jullie werkzaamheden. Er zijn talloze boeken over geschreven en ook in bijvoorbeeld de film “The Accountant” uit 2016 werd de wet van Benford daar gebruikt om fraude aan te tonen: Ben Affleck zag dat de fraudeur een duidelijke voorkeur had voor het getal 3.
De wet van Benford is vernoemd naar de Amerikaanse fysicus Frank van Benford die hierover publiceerde in 1938. Hij is echter niet de feitelijke ontdekker, dat is namelijk de Canadees-Amerikaanse wiskundige Simon Newcomb in 1881, die opmerkte dat in logaritmetabellen de eerste pagina’s veel meer versleten waren dan de andere pagina’s. Benford wist de herontdekking echter veel beter te vermarkten.
Verdeling van cijfers
Voor wie nog onbekend is met de wet van Benford, het beschrijft de frequentieverdeling van het begincijfer van getallen in grote dataverzamelingen. Hieruit blijkt dat het begincijfer 1 30% voorkomt, het begincijfer 2 18% en de rest van de begincijfers in een glijdende schaal nog veel minder waarbij de 9 tenslotte nog maar in zo’n 5% van de gevallen voorkomt. Zie onderstaande grafiek:
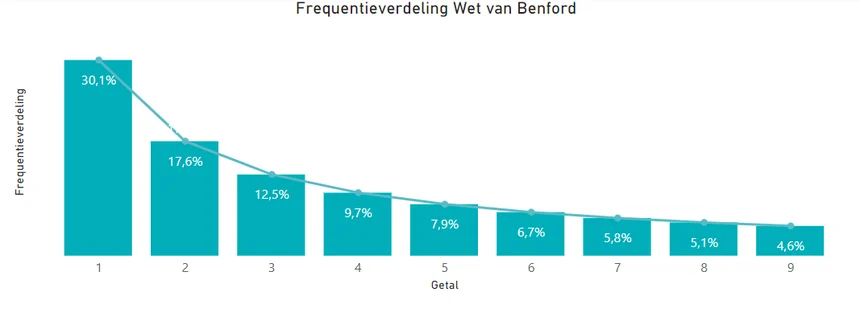
Deze frequentieverdeling wordt berekend op basis van deze door Newcomb bedachte formule:
Als het getal N het eerste cijfer van een getal is, is de kans dat dit getal voorkomt gelijk aan:
log( N + 1) − log( N )
De wet van Benford gaat echter niet op voor elke dataset. Benford merkte in datasets op dat hoe willekeuriger en hoe groter het bereik van de grootte van de getallen zijn, hoe dichter de kansverdeling bij ‘zijn’ formule lag.
De frequentieverdeling kan gebruikt worden om fraude op te sporen als ervan uit wordt gegaan dat fraudeurs die zelf getallen moeten verzinnen hierbij een uniforme verdeling toepassen of voorkeursgetallen hebben zoals in “The Accountant”. Kanttekening daarbij is dat een fraudeur die kennis heeft van de wet van Benford, ongetwijfeld de veronderstelde verdeling zal toepassen bij het maken van fictieve cijfers.
Hoewel de meningen verdeeld zijn of de wet nu wiskundig bewezen is of niet, uit empirisch onderzoek blijkt dat deze wet wel verrassend vaak opgaat. Zo gaat deze op in onder meer de volgende datasets:
- Adressen
- Lengte van rivieren
- Bevolkingspopulaties
- Openstaande saldi debiteuren
De onderstaande verdeling heb ik bijvoorbeeld gemaakt met het eerste getal van het aantal inwoners per land. De twee frequentieverdelingen komen aardig bij elkaar in de buurt, al zou deze officieel verworpen moeten worden. De afwijkingen zijn te groot door het geringe aantal landen in de populatie, namelijk 237.
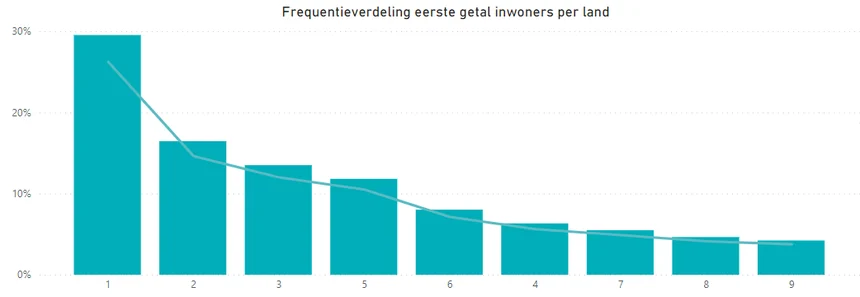
Financiële gegevens
In financiële datasets kan ook de betrouwbaarheid worden beoordeeld aan de hand van de wet van Benford. Als getallen verzonnen moeten worden, bijvoorbeeld in het geval van fraude, zullen mensen trachten een willekeurige verdeling van de getallen te maken. Een flinke afwijking in de frequentieverdeling kan erop wijzen dat er iets niet helemaal in de haak is.
Tot op heden is er nog geen eenduidig wiskundige verklaring gevonden voor het feit dat sommige datasets zich houden aan deze wet van Benford, alhoewel het bewijs dat Hill in 1995 leverde als baanbrekend wordt gezien. Het gaat echter te ver voor dit artikel om dit bewijs hier uiteen te zetten, maar ook ik ben van mening dat de wet meer op feiten dan op toeval berust.
In de ontwikkeling van Analytics AI gaan we de Wet van Benford dan ook zeker ondersteunen zodat je de frequentieverdeling kunt toepassen op jouw datasets.